setwd("~/Curso_R/Estadistica_basica")2 Análisis de datos
2.1 Importando datos en R
Antes de ingresar nuestros datos, es muy importante indicar a R cuál será nuestro directorio de trabajo o también llamado Working Directory. Es decir, debemos establecer la carpeta dentro de la cual se encuentran los archivos a utilizar, y donde se exportarán los que generes durante tu trabajo.
R toma automáticamente un directorio en el cual trabajar y puedes saber cual es con la función getwd().
Existen algunas formas de establecer el lugar de trabajo. La primera es de manera manual:
Nota que el símbolo ~ se encuentra al inicio del directorio escrito. Este símbolo reemplaza al resultado obtenido de la función getwd.
La segunda manera de establecer el directorio es presionando las teclas Ctrl+Shift+H. Inmediatamente se abrirá una ventana en la que podrás seleccionar tu directorio manualmente.
2.1.1 Archivos csv
Puedes descargar el achivo utilizado en este tutorial desde este link . Antes de importar este u otro archivo debes tener claro cuál es el tipo de extensión, ya que diferentes formatos implican diferentes funciones para importarlos.
Tanto los archivos txt y xlsxl resultan un poco más complicados de leer e incluso necesitan la instalación de otros paquetes como readxl. Por otro lado, los archivos csv (comma separated values) con los que trabajarás en esta clase, se pueden importar de esta manera:
data <- read.csv("osos_hema.csv")Asegúrate que el archivo osos_hema.csv se encuentra en el directorio que indicaste previamente.
Una vez que hayas importado el archivo, lo puedes ver como data frame en el panel Environment. Puedes hacer clic sobre el objeto e inspeccionarlo brevemente.
Repasa las funciones que aprendiste en Capítulo 1 para obtener datos más específicos sobre el objeto data.
head(data)
summary(data)
str(data)Observa que hay una gran cantidad de datos faltantes, NA’s. ¿Son estos datos faltantes un problema para calcular la media y mediana de la columna colesterol?
mean(data$colesterol)
## [1] NA
median(data$colesterol)
## [1] NALos resultados muestran que no es posible calcular estas medidas de tendencia sin haber limpiado el data frame. Para poder hacerlo, es aconsejable elegir las columnas de interés y realizar la limpieza de NA’s únicamente en éstas.
2.2 Manipulación de data frames
Ahora aprenderás a manipular los datos que serán analizados en la sección 2.3, e investigarás si existe alguna diferencia entre la media de colesterol de machos y hembras, y si la hubiera, testearás si esta disimilitud es estadísticamente significativa realizando la prueba de hipótesis estadística T de Student.
Por último, investigarás si existe correlación entre los niveles de colesterol y triglicéridos en ambos sexos. Para esto necesitas algunos paquetes.
library(tidyverse)
library(rafalib)Para deshacerte de los NA's puedes extraer las columnas de interés de una manera parecida a la que has aprendido anteriormente.
lipidos <- data[ ,c("colesterol", "trigliceridos", "sexo")]
lipidos <- na.omit(lipidos)
# También puedes buscar las filas que poseen NA’s
which(is.na(data$colesterol))¿Cómo podrías deshacerte de los NA's utilizando which(is.na())?
2.2.1 pipes
Ahora usarás una de las funciones más populares del paquete magrittr (parte de tidyverse), llamado pipe y escrito como %>%. Este operador se utiliza mucho en lenguaje de programación ya que simplifica la unión de funciones. Sin embargo, desde la versión de R 4.1.0, se introdujo el operador nativo |>. El uso de ambos depende del contexto en el cual son implementados como se discute en este artículo, y hay un gran resumen del uso de cada uno aquí.
Sea cual sea tu elección, ambos pipes se traducen a lenguaje común como “después”, y se utilizan para pasar el output de una primer función hacia una segunda, tercera, etc.
Puedes aprovechar esta función para simplificar la escritura del código para extraer ciertas columnas de data.
# Extrae las columnas de lipidos y sexo
lipidos <- data %>%
dplyr::select(colesterol, trigliceridos, sexo) %>%
na.omit()
# Extrae las columnas de compuestos nitrogenados y sexo
nitrogenados <- data %>%
dplyr::select(proteina, bun, sexo) %>%
na.omit()Ahora el código es más fácil de interpretar y este se lee como: “toma el objeto data; después selecciona las columnas colesterol, triglicéridos y sexo; después omite los NA’s”. Esto se lee de igual manera para el objeto nitrogenados.
2.2.2 Manipulación semi-avanzada
Puedes hacer mucho más con este set de datos hipotético que puedes aplicar en tu propia investigación.
# Agrega una columna con la relación proteina/bun
data %>%
dplyr::select(proteina, bun, sexo) %>%
na.omit() %>%
mutate(proteina_bun_ratio = proteina / bun) %>%
head()
## proteina bun sexo proteina_bun_ratio
## 1 12.3057808 10.981548 hembra 1.12058703
## 2 14.5265548 16.572126 hembra 0.87656556
## 3 2.6605606 3.772625 hembra 0.70522797
## 4 12.8490715 8.128610 macho 1.58072177
## 5 0.9260416 12.113160 macho 0.07644922
## 6 3.1239402 17.496444 hembra 0.17854715
# Agrega categorías por rangos
data %>%
dplyr::select(proteina, bun, sexo) %>%
na.omit() %>%
mutate(categoria_bun = case_when(
bun < 15 ~ "Bajo",
bun >= 15 & bun <= 20 ~ "Normal",
bun > 20 ~ "Alto")) %>%
head(n = 10)
## proteina bun sexo categoria_bun
## 1 12.3057808 10.981548 hembra Bajo
## 2 14.5265548 16.572126 hembra Normal
## 3 2.6605606 3.772625 hembra Bajo
## 4 12.8490715 8.128610 macho Bajo
## 5 0.9260416 12.113160 macho Bajo
## 6 3.1239402 17.496444 hembra Normal
## 9 7.3849111 8.768299 hembra Bajo
## 10 4.6996813 11.005729 macho Bajo
## 14 21.7550518 18.432460 hembra Normal
## 15 15.9212473 18.828829 macho Normal¿Cómo harías para seleccionar y guardar únicamente los valores normales en nuevo data frame?
2.3 Estadística básica en R
Puedes realizar una exploración rápida de tus datos antes de iniciar análisis específicos. Observemos en un scatterplot como se distribuyen los datos.
plot(data)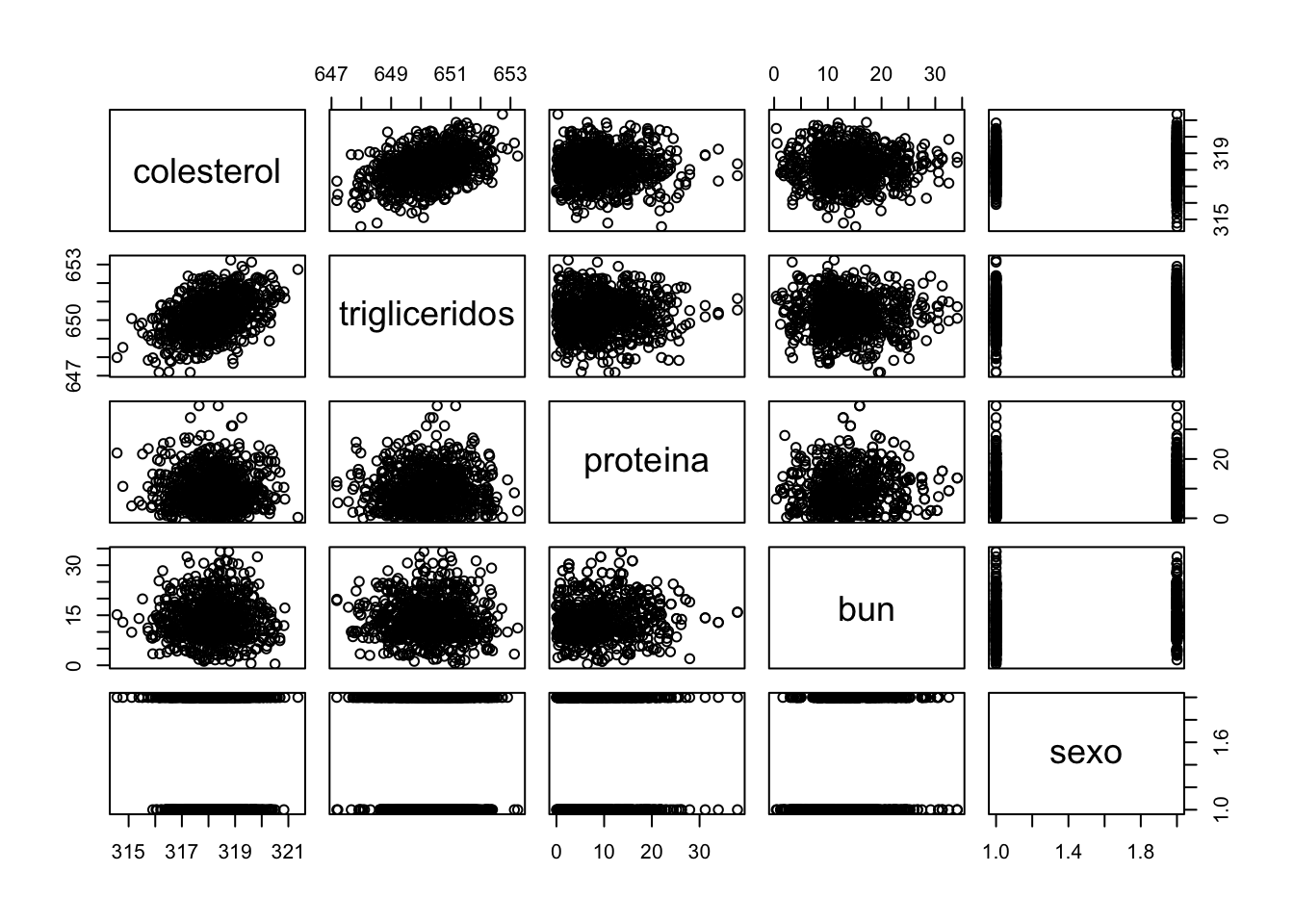
2.3.1 Correlación
Parece ser que hay algún tipo de relación entre las variables de colesterol y triglicéridos. Podemos utilizar la función cor para determinar si de hecho existe alguna correlación.
cor(lipidos$colesterol, lipidos$trigliceridos)
## [1] 0.4223668Este resultado, sin embargo, no es muy claro pero recuerda que no estamos separando estos datos basados en otra variable como edad o sexo, que podrían tener una influencia en este resultado. Además, por default cor utiliza el método de Pearson. ¿Cambiaría este resultado en base al uso de otro método?
Calcula la correlación de estas variables mediante el método de Spearman.
Ahora apliquemos más funciones de dplyr junto con los pipes para calcular la correlación en base al sexo.
lipidos %>%
group_by(sexo) %>%
summarise(cor = cor(colesterol, trigliceridos))
## # A tibble: 2 × 2
## sexo cor
## <chr> <dbl>
## 1 hembra 0.340
## 2 macho 0.473También puedes utilizar ggplot2 para graficar esta posible correlación.
lipidos %>%
ggplot(aes( x = colesterol, y = trigliceridos, color = sexo)) +
geom_point(alpha = 0.5) +
geom_smooth(method = "lm", se = FALSE) +
labs( x = "colesterol (mg/dl)", y = "triglicéridos (mg/dl)") +
theme_bw()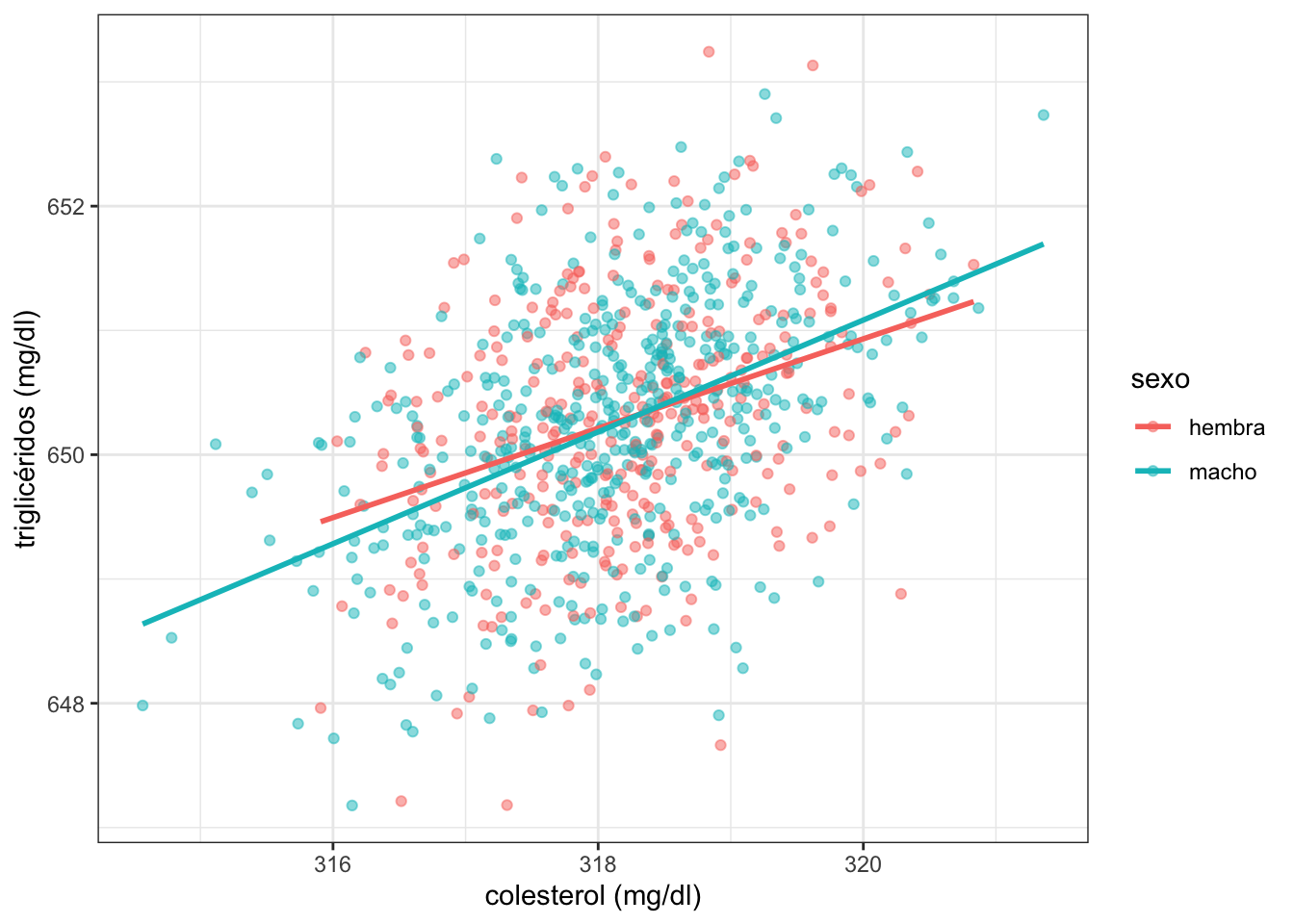
2.3.2 Diferencias de medias
Ahora utiliza el objeto nitrogenados e inspecciona en detalle alguna diferencia entre machos y hembras.
nitrogenados %>%
dplyr::select(bun, sexo) %>%
group_by(sexo) %>%
summarise(media = mean(bun),
mediana = median(bun),
desv_est = sd(bun))Estas posibles diferencias también pueden ser observadas mediante un gráfico de caja y bigotes.
boxplot(nitrogenados$bun ~ nitrogenados$sexo)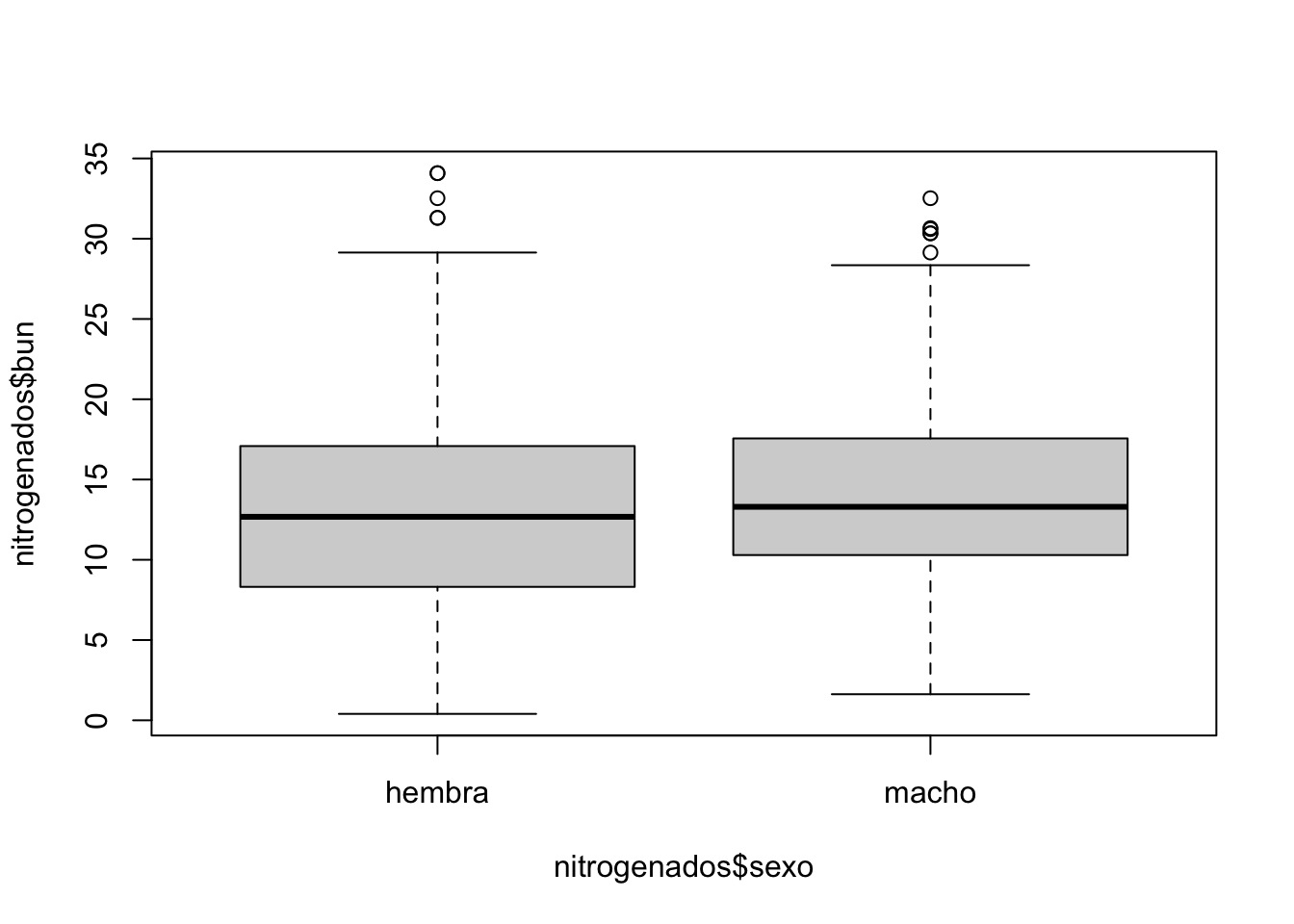
boxplot(nitrogenados$proteina ~ nitrogenados$sexo)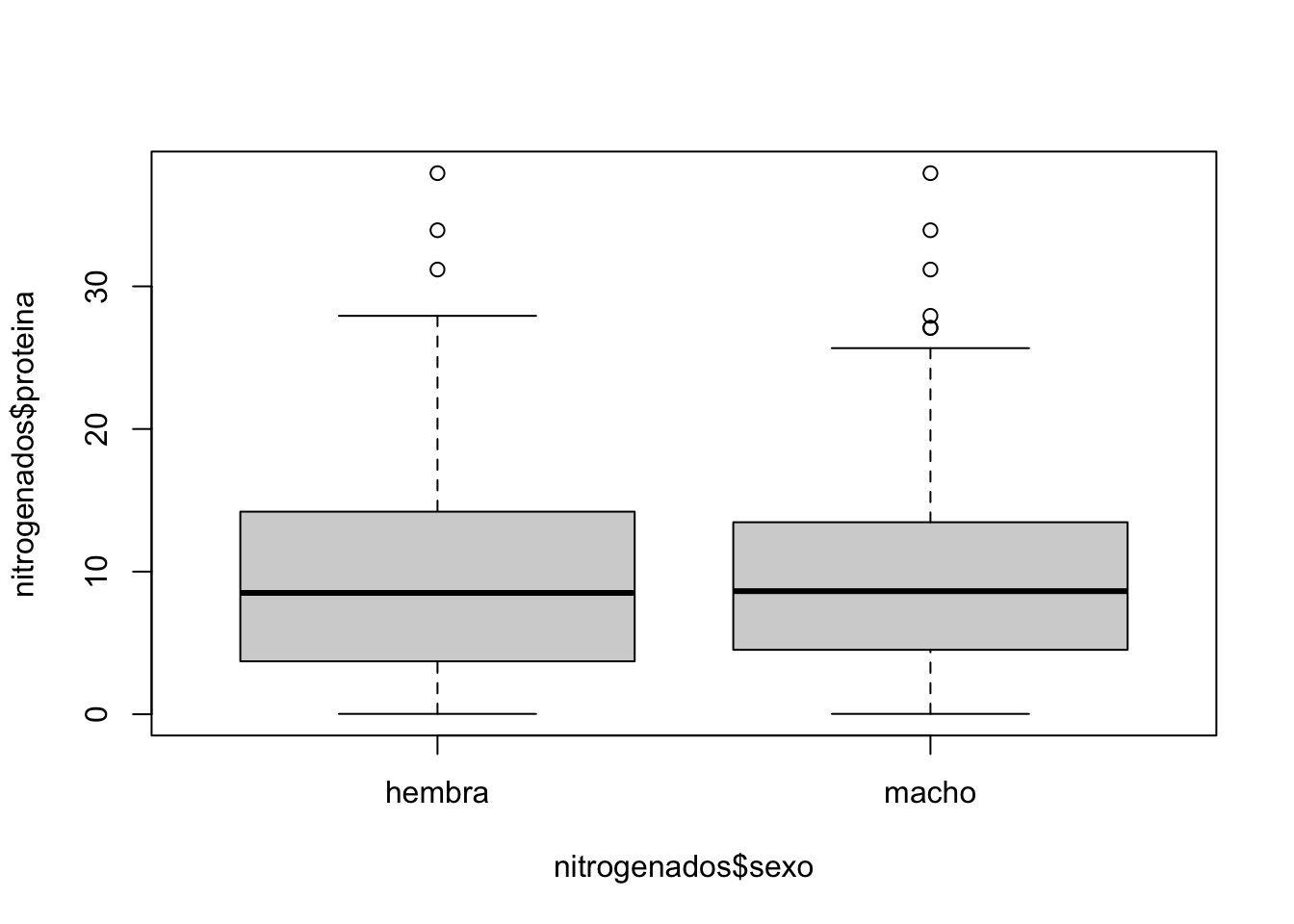
La diferencia de medidas de tendencia entre sexos no es clara. Sin embargo, ¿cómo podemos saber que esta diferencia es o no estadísticamente significativa?
Aunque a fines de este ejemplo, utilizaremos el test de Student para calcular el valor p, es necesario aclarar que no profundizaremos en detalles matemáticos o discutiremos sobre que tipos de test podrían contestar esta pregunta de mejor manera. Si deseas tener más conocimiento sobre temas estadísticos, dirígete a la sección de Fuentes de este documento y descarga los libros y documentos que sean de tu interés.
Primero, debemos observar si nuestros datos siguen una distribución normal. Para esto utilizaremos funciones base de R y además la función mypar() del paquete rafalib que instalamos previamente.
mypar(1,2)
# Grafica un histograma
hist(nitrogenados$bun, main = "Distribución de valores de Urea en sangre")
# y además
qqnorm(nitrogenados$bun)
qqline(nitrogenados$bun)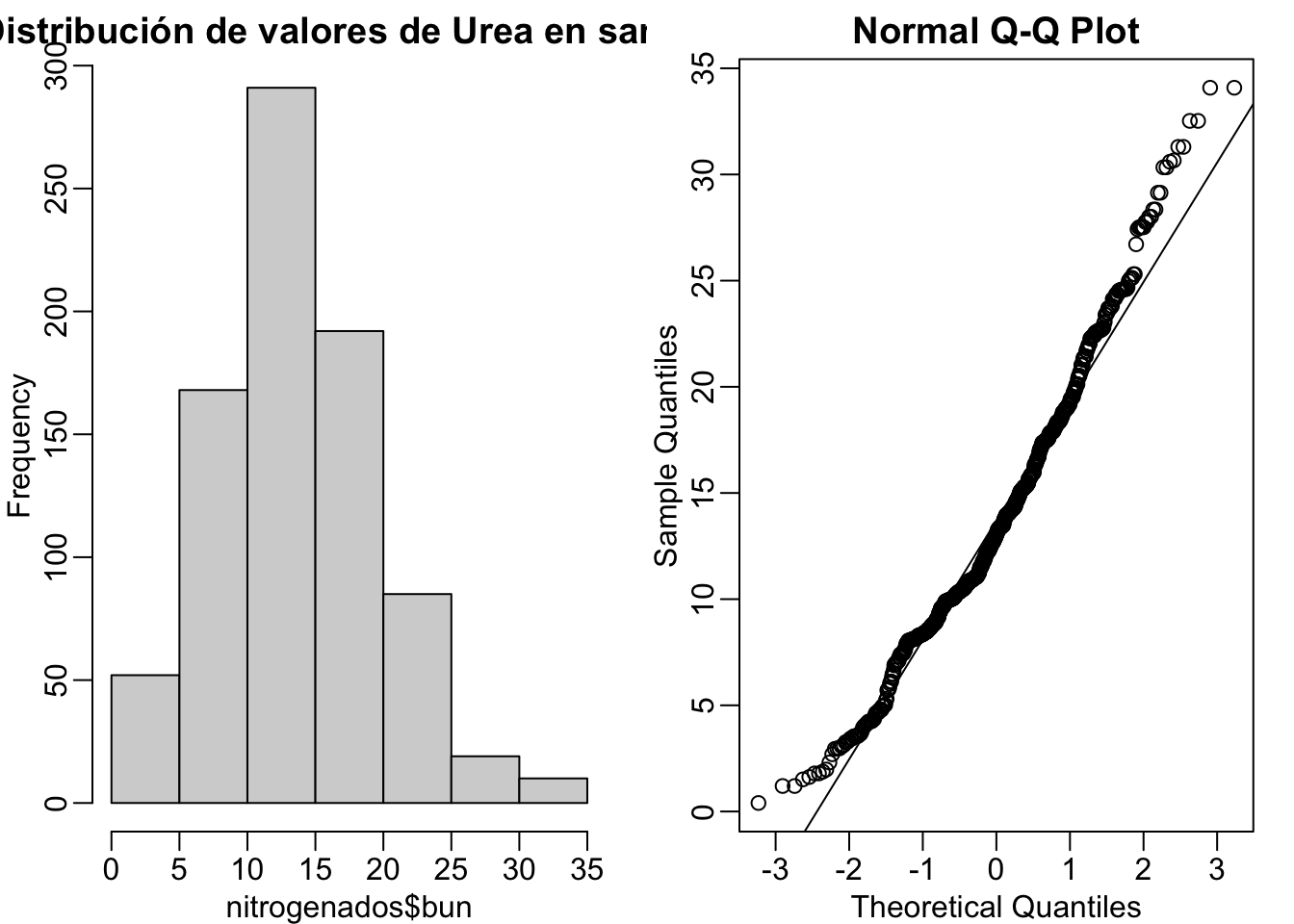
Si deseas saber más sobre el significado de los Q-Q plots, ingresa aquí.
Si quieres aumentar la confianza sobre la normalidad de tu set de datos, puedes utilizar la función shapiro.test.
shapiro.test(nitrogenados$bun)
##
## Shapiro-Wilk normality test
##
## data: nitrogenados$bun
## W = 0.97721, p-value = 5.523e-102.4 T de Student
Ahora que tienes evidencia de que los niveles de urea en sangre se aproximan a una distribución normal, puedes calcular el valor p. Primero necesitas subdividir al objeto nitrogenados.
# Crea un objeto con los machos
bun_m <- nitrogenados %>%
filter(sexo == "macho") %>%
dplyr::select(bun) %>% unlist()
# Ahora uno con las hembras
bun_h <- nitrogenados %>%
filter(sexo == "hembra") %>%
dplyr::select(bun) %>% unlist()¿Cómo fueron almacenados los objetos col_m y col_h?. Lee sobre unlist en la sección de Ayuda.
Puedes entonces realizar la prueba T de Student con una sola línea de comando.
t.test(bun_h, bun_m, var.equal = T)
#Si solo quieres obtener el valor de p
t.test(bun_h, bun_m, var.equal = T)$p.valueEl p-value = 0.002837017, quiere decir que hay muy baja probabilidad de que la diferencia de medias en los niveles de urea en sangre se deba a un error de muestreo o al azar. Consecuentemente, la hipótesis nula queda rechazada y aceptamos la hipótesis alternativa.
2.5 Análisis de Componentes Principales
Este método de reducción dimensional incluye el análisis de valores propios (eigenvalues) y vectores propios (eigenvectors) de una matriz de covarianza o correlación. Sin embargo, para los propósitos de este curso aprenderás los conceptos básicos y necesarios para realizar este análisis multivariado. Te recomiendo que hagas una lectura a fondo de este tema utilizando la bibliografía que puedes encontrar en 2.7, si quieres utilizar este método para publicaciones científicas.
Por lo pronto, empieza instalando los paquetes necesarios para esta sección e importando otro archivo hipotético de un segundo análisis de sangre que puedes descargara desde aquí.
library(factoextra)
library(ggfortify)
data_pca <- read.csv("osos_hema_pca.csv")Hay muchos paquetes que incorporan funciones para realizar un PCA, pero para este curso introductorio sugiero que te familiarices con la función prcomp del paquete stats y algunas de factoextra para visualización.
prcomp(data_pca[,1:4] , center= TRUE, scale=TRUE)¿Por qué no puedes correr este código? Recuerda que el set de datos que importamos, no fue limpiado, y al tener NA's, los análisis matemáticos no son posibles. Asegúrate de limpiarlo antes de proceder.
# Limpia los datos
clean_data <- data_pca %>% na.omit()
# PCA
osos_pca <- prcomp(clean_data[, 1:4] , center= TRUE, scale=TRUE)Es muy importante tener en cuenta que los argumentos center y scale deben ser utilizados siempre. Así eliminarás sesgos sistemáticos asegurándote que la estructura de tus datos se basen en la covarianza/varianza, y además estandarizas los datos para evitar que la posible diferencia de escalas no afecten el cálculo.
Ahora puedes analizar los resultados del PCA de varias maneras y cada una de ellas te proporcionará con información valiosa para que entiendas los factores que contribuyen a la aparición de patrones y estructuras en los datos.
2.5.1 Entendiendo el PCA
Empieza por ver un resumen del análisis.
summary(osos_pca)
## Importance of components:
## PC1 PC2 PC3 PC4
## Standard deviation 1.6858 0.9817 0.43995 0.02920
## Proportion of Variance 0.7105 0.2409 0.04839 0.00021
## Cumulative Proportion 0.7105 0.9514 0.99979 1.00000Puedes notar que la proporción de varianza en el primer componente principal (PC1) es del 71.05% y en el PC2 es 24.09%, es decir que juntos explican el 95.14% de varianza total de los datos. Puedes visualizar qué componentes principales explican la mayor parte de la varianza, lo que te permitirá decidir cuantos componentes deberiás elegir para tus análisis posteriores.
# Genera un scree plot
fviz_eig(osos_pca, addlabels = TRUE,
barfill = "gray70", barcolor = "black")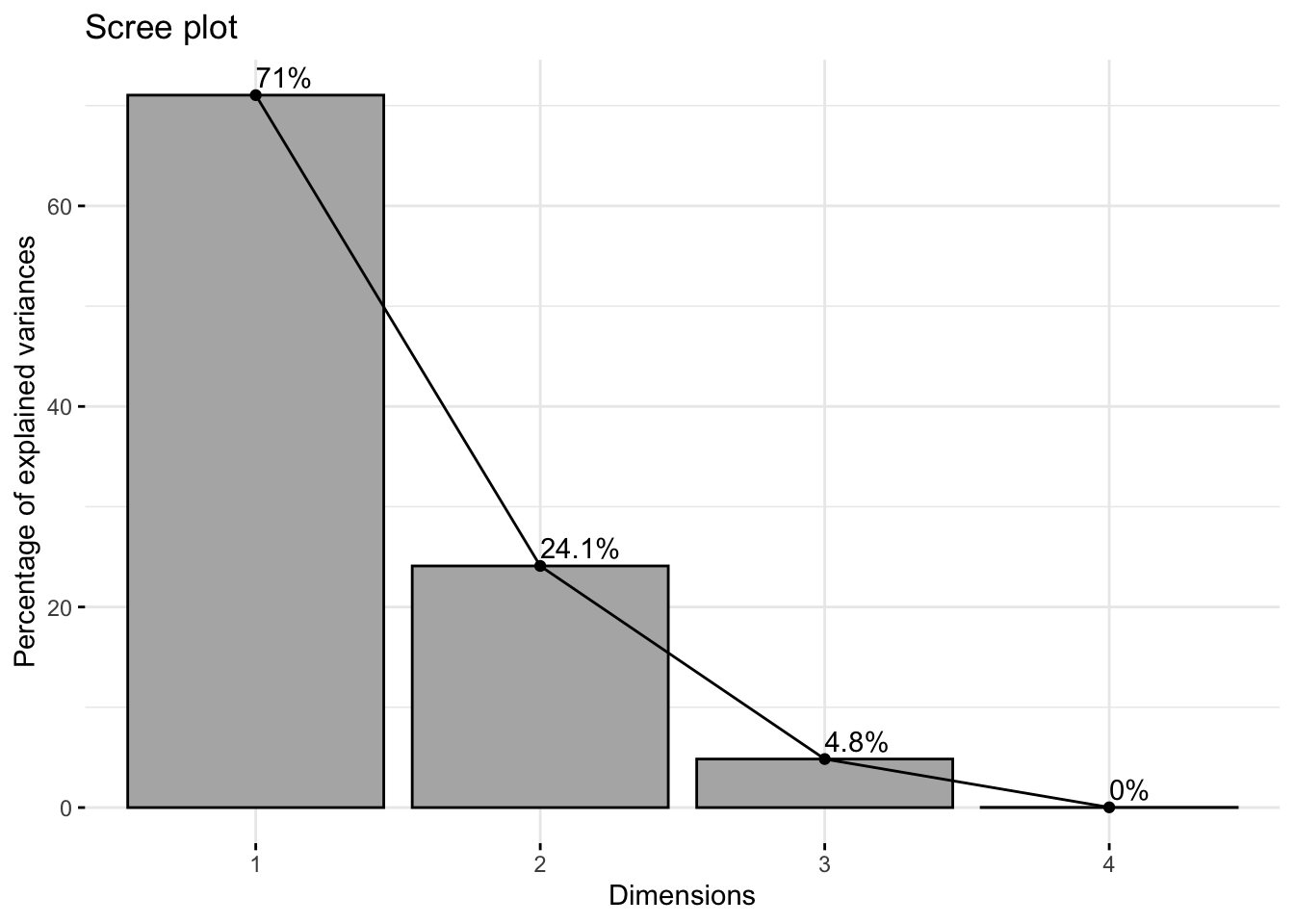
Los valores mostrados en el scree plot también puedes obtenerlos desde el objeto de esta manera:
get_eigenvalue(osos_pca)
## eigenvalue variance.percent cumulative.variance.percent
## Dim.1 2.8418189096 71.04547274 71.04547
## Dim.2 0.9637712653 24.09428163 95.13975
## Dim.3 0.1935573660 4.83893415 99.97869
## Dim.4 0.0008524591 0.02131148 100.00000Ahora sabes cuantos componentes deberías elegir, pero, ¿cuáles son las variables que están más fuertemente asociadas con cada componente principal?
osos_pca$rotation
## PC1 PC2 PC3 PC4
## colesterol 0.5837967 -0.013514952 -0.3992519 0.706821577
## trigliceridos 0.5838873 -0.002060441 -0.3984143 -0.707345345
## proteina 0.4585282 -0.569329319 0.6823478 -0.004177978
## bun -0.3286472 -0.821995880 -0.4650435 -0.006954500Puedes visualizar esta contribución de la siguiente manera:
fviz_pca_var(osos_pca,
col.var = "contrib",
gradient.cols = c("#440D54", "#39568C", "#54C667"),
repel = TRUE)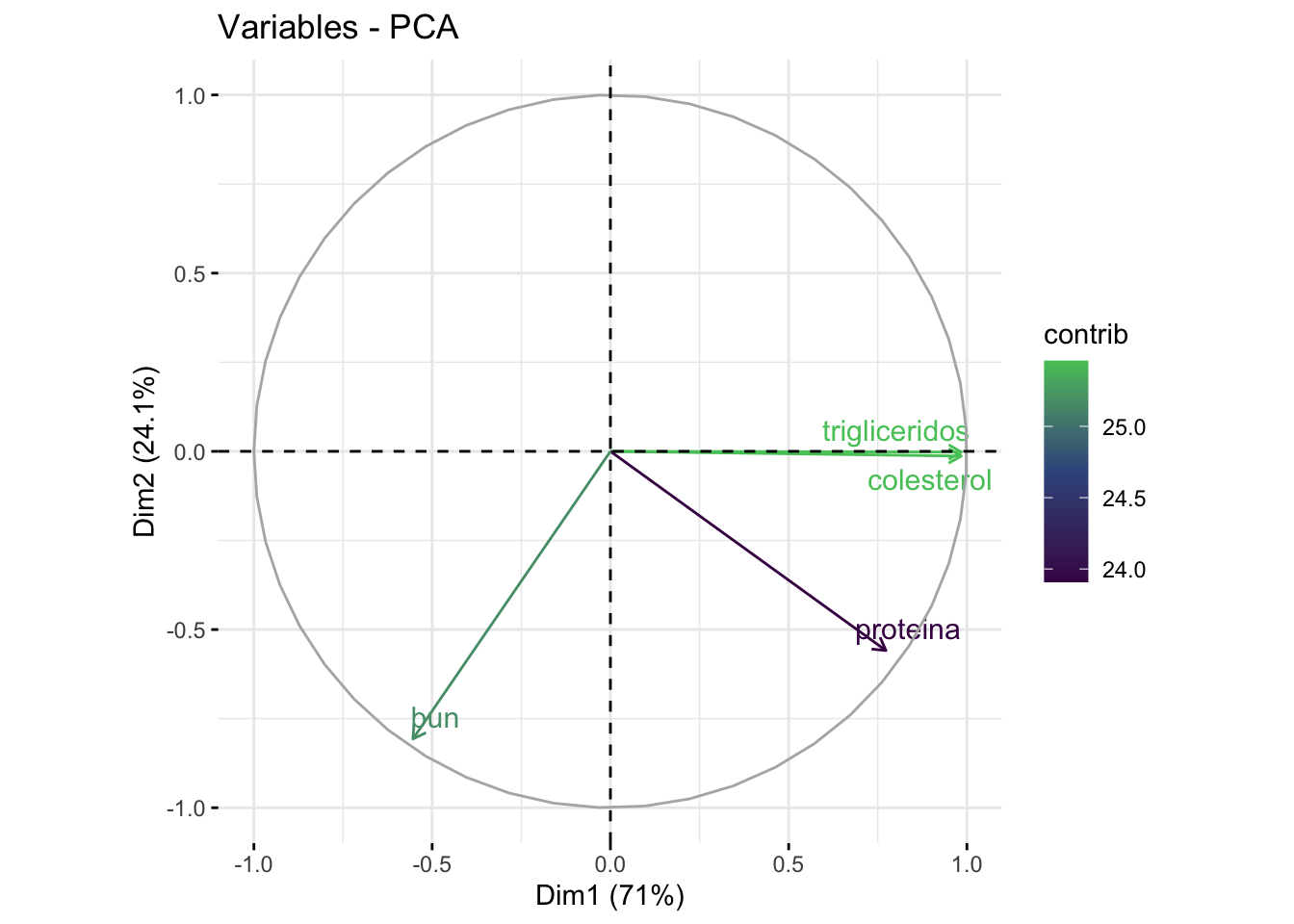
Los colores utilizados en este gráfico los he extraído del paquete viridis, que ayudan a mejorar la representación de los datos y son amigables con gente daltónica.
2.5.2 Biplots
Ahora puedes crear un biplot, un tipo de gráfica típica de este análisis que contiene al score plot, es decir a los datos proyectas en dos componentes principales, y el loading plot, que representa la contribución de cada variable.
fviz_pca_biplot(osos_pca,
geom.ind = "point",
pointshape = 21,
pointsize = 3.5,
fill.ind = clean_data$sexo,
label = "var",
repel = TRUE,
legend.title = "Sexo osos",
title = "") +
theme_light()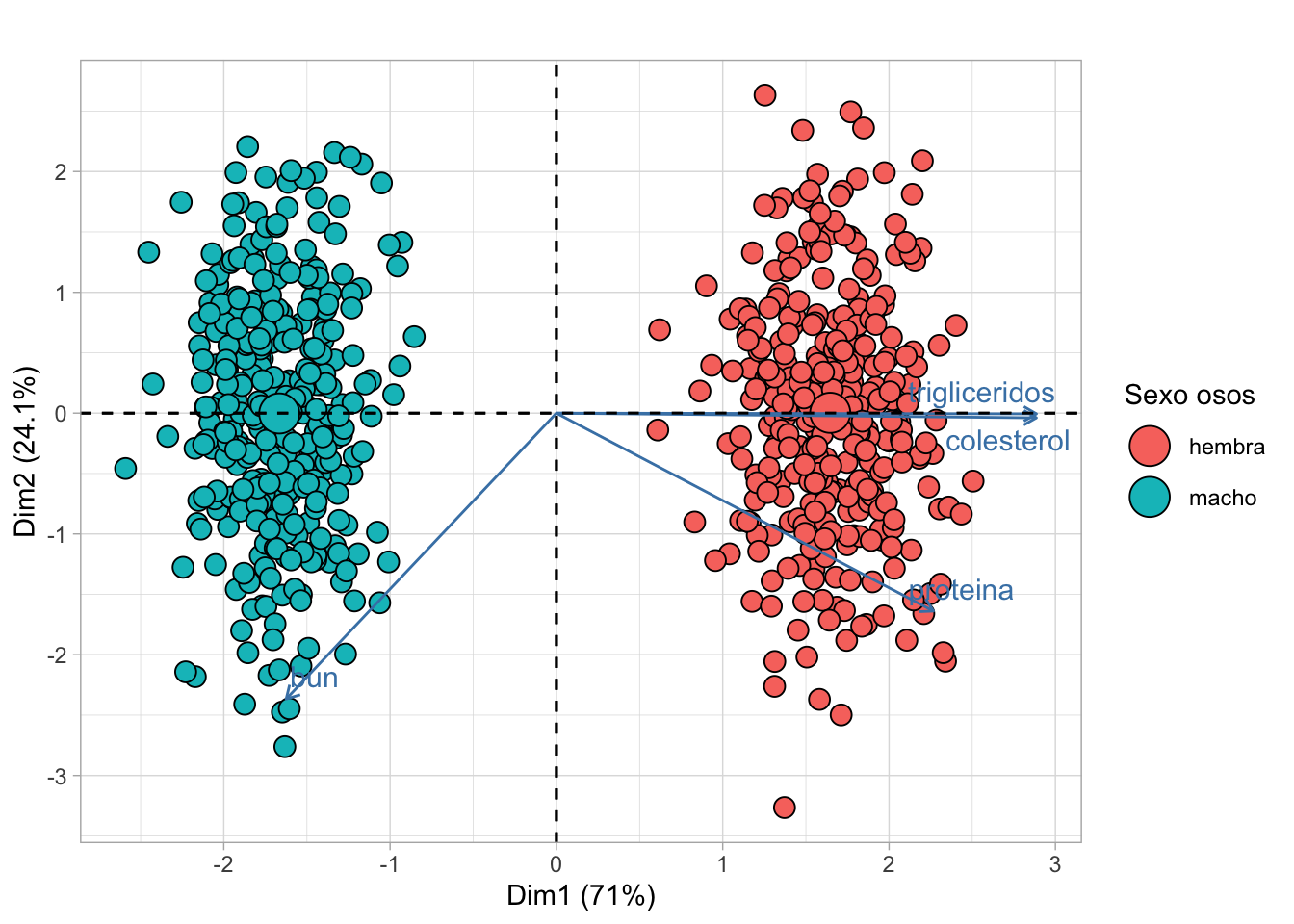
2.6 Personalizando gráficos con ggplot2
Existen tres sistemas de plotting en R, base plotting, el paquete lattice y ggplot2. Por ahora nos concentraremos en indagar en algunas de las tantas opciones de personalización que nos ofrece ggplot2 y de otros paquetes que interactúan con éste.
2.6.1 Plotly
Imaginemos que una vez concluidos nuestros análisis, estamos disconformes con ellos y creemos que puede deberse a un error en los datos. ¿Como podríamos identificar entre tantos valores a aquel que genera un error en el cálculo de estadísticos? Para generar el gráfico que nos puede ayudar a responder esta pregunta, necesitaremos descargar primeramente el paquete plotly.
library(plotly)
# Crea un objeto que contenga un ggplot de nuestro dataset lipidos.
lipidos_valores <- lipidos %>%
ggplot(aes(x = colesterol, y = trigliceridos, colour = sexo)) +
geom_point() +
# Cambia el temadel plot
theme_light() +
# Cambia los nombres de los ejes
labs( y = "Triglicéridos", x = "Colesterol")
# !Observa el gráfico interactivo!
ggplotly(lipidos_valores)Este gráfico interactivo aparecerá en la pestaña Viewer y te permitirá ubicarte sobre cualquier punto del scatterplot y observar su valor en el eje de coordenadas. Esto será muy útil más adelante para deshacernos de outliers en los análisis espaciales.
2.6.2 Paquetes que interactúan con ggplot2
2.6.2.1 ggExtra
Este es un paquete que mejora la visualización de gráficas adjuntando histogramas, boxplots y plots de densidad hacia los márgenes de una gráfica realizada en ggplot2.
library(ggExtra)
# ¿Por qué crees que almacenamos el siguiente gráfico como un objeto?
g <- ggplot(lipidos, aes(colesterol, trigliceridos, colour=sexo)) +
geom_point() +
# Agrega regresiones lineales
geom_smooth(method = "lm", se = F) +
# Agrega un título al plot
labs(title = "Correlación y Distribución \nde lípidos") +
# Cambia el tema del plot
theme_bw () +
# La posición de la leyenda y el tamaño de la letra
theme(legend.position = "bottom",
text = element_text(size = 15))
# Crea un gráfico con ggExtra
ggMarginal(g, type = "histogram", fill = "transparent")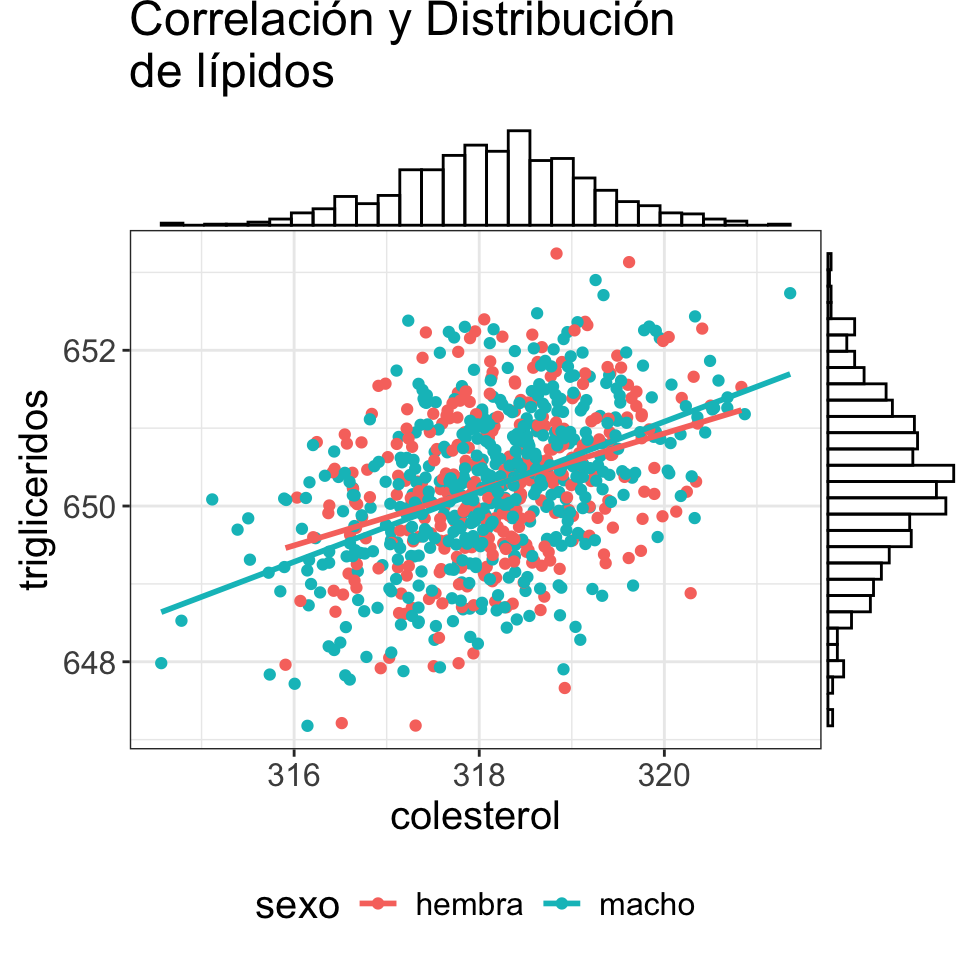
Lee el apartado de ayuda de ggMarginal y grafica un diagrama de caja y bigotes en lugar de un histograma.
2.6.3 Exportando figuras
Existen algunas opciones para exportar los gráficos generados en R, una de ellas es ggsave. Por default ggsave exporta la última figura generada, pero también puedes guardar cualquier imagen como un objeto y exportarla en cualquier punto de tu trabajo. Exportar utilizando esta función te da mucho control sobre la calidad y extensión de la figura. Esta guía te da muchos más detalles sobre los argumentos que puedes utilizar dentro de la función. Para mantener las cosas sencillas en este curso, utiliza el siguiente código para exportar la última imagen generada
ggsave("lipidos_osos.png",
width = 5,
height = 5,
units = "cm",
dpi = 72)2.7 Fuentes
Este capítulo fue tomado y adaptado de diversas fuentes, siendo R for Data Science, el curso gratis de edX Statistics and R, Linear Algebra for Data Science with examples in R, Plotting PCA, y Principal Component Methods in R: Practical Guide las más grandes influencias de este trabajo.
Tanto el análisis estadístico como la creación de gráficos utilizando ggplot2 son temas muy amplios para los cuales existen una amplia gama de recursos en internet. En cuanto a la parte estadística, he hecho una recopilación muy breve de libros que abordan estos temas, así como también sobre la investigación reproducible, su importancia, y como llevarla a cabo en R. Para acceder a estos recursos haz clic aquí.
Finalmente, puedes profundizar más en el uso de ggplot2 ingresando a: Data Visualization with R , Top 50 ggplot2 Visualizations y Data visualization with ggplot2.