Obten el objeto zebras.transf
zebras.transf <- spTransform(zebras.proj,
CRS("+proj=lcc +lat_1=20 +lat_2=-23 +lat_0=0 +lon_0=25 +x_0=0 +y_0=0 +ellps=WGS84 +datum=WGS84 +units=m +no_defs"))4 Áreas de vida
La estimación de áreas de vida es una parte fundamental, pero no la única, en el estudio de la ecología y etología de los animales, y los artículos científicos de Kays et al. (2015), Abrahms et al. (2021), y Silva et al. (2022) son una excelente fuente de información si estás involucrándote en el mundo de la ecología de movimiento. Si bien existen diversos métodos por los cuales se pueden estimar dichas áreas, en este módulo aprenderás sobre métodos tradicionales ampliamente utilizados y que serán comparados más adelante con nuevos métodos en el paquete ctmm.
4.1 adehabitatHR
El paquete adeHabitatHR es uno de cuatro paquetes que hace unos años formaban parte del paquete ya deprecado adehabitat, y se especializa en el análisis de áreas de vida. Este paquete, sin embargo, se enfrenta a un riesgo a futuro ya que otros paquetes utilizados dentro de la disciplina del análisis espacial, dependían en gran medida de los paquetes raster, rgdal, rgeos, y sp, que fueron reemplazados en el 2023 por sf y terra. sp es el único que se adaptó a esta transición y adoptó funciones del paquete sf Sin embargo, adehabitatHR no se adaptó a esta transformación y depende de la instalación de estos paquetes que ya no reciben mantenimiento.
A pesar de esto, aprender sobre adeHabitatHR es aún necesario ya que no existe, a la fecha, un paquete que incorpore todas las utilidades que éste lo hace.
Ahora estimarás el área de vida de las zebras que fueron extraídas en el objeto zebras.transf en la Sección 3.2.
Obten el objeto
4.2 Minimum Convex Polygon (MCP)
4.2.1 Zebras en África
Este método es de los más sencillo para dibujar los límites de distribución de un animal. Aunque su uso original Carl O. Mohr (1947) fue destinado a la identificación de animales recapturados en una malla de captura.
El uso del MCP es limitado ya que este describe el alcance de la distribución de ubicaciones de un individuo, mas no la verdadera área de vida del animal bajo estudio. Para una discusión más detallada sobre esto puedes leer Signer y Fieberg (2021), y un debate profundo sobre rangos y ocurrencia de distribución en C. H. Fleming et al. (2016).
A pesar de lo anteriormente mencionado, obtener el área del polígono y el poder ubicarlo sobre un mapa, nos permite observar a grosso modo el espacio y hábitat que ocupa cierto ejemplar.
library(adehabitatHR)
library(sf)
zebras.mcp <- mcp(zebras.transf[, "identifier"], percent= 100,
unin="m", unout= "ha")
Ejercicio
Ahora intenta con distintos porcentajes y observa las diferencias en tamaños de área.
Si bien puedes utilizar funciones base de R para graficar estos polígonos, aprovecha la interacción de estos paquetes con sf y ggplot2 para obtener un gráfico más estético.
library(ggplot2)
ggplot() +
geom_sf(data = st_as_sf(zebras.mcp), aes(fill = id),
alpha = 0.2) +
geom_sf(data = st_as_sf(zebras.transf), aes(colour = identifier)) +
coord_sf() +
theme_bw()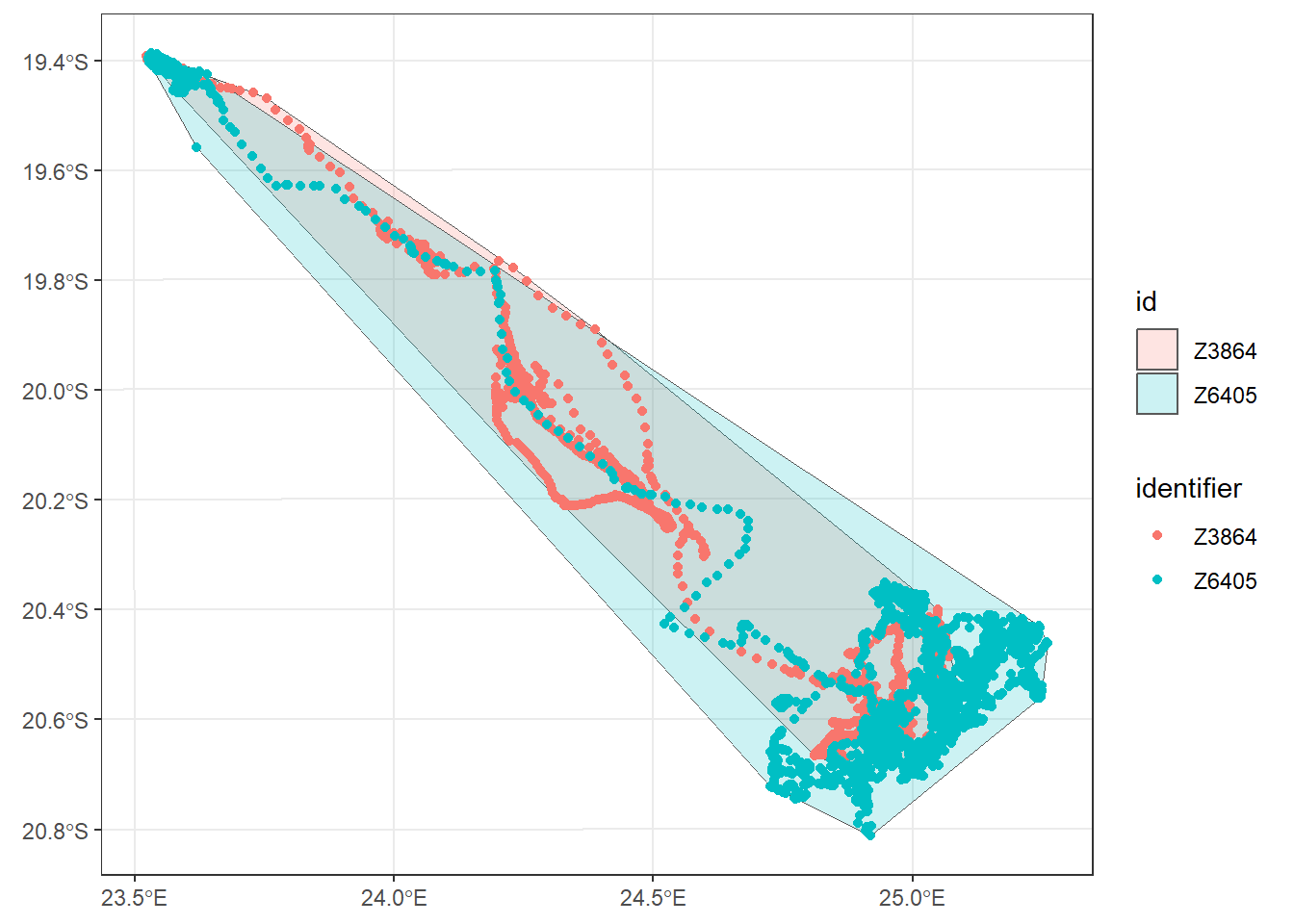
También puedes exportar estos polígonos con extensión kml para que puedas importarlos en Google Earth o cualquier software de tu preferencia.
st_write(st_as_sf(zebras.mcp), "zebras.kml", delete_layer = TRUE)4.2.2 Animales hipotéticos
Como caso de estudio, e intentando que mejores en el flujo de trabajo de estos análisis, creé un set de datos de tres mamíferos hipotéticos en la zona Norte de Loreto - Perú, y lo puedes descargar aquí.
mamiferos <- read.csv("mamiferos.csv")Como siempre, haz una exploración rápida de este objeto y grafica los puntos satelitales rápidamente.
plot(mamiferos[, c("longitude", "latitude")], pch=20)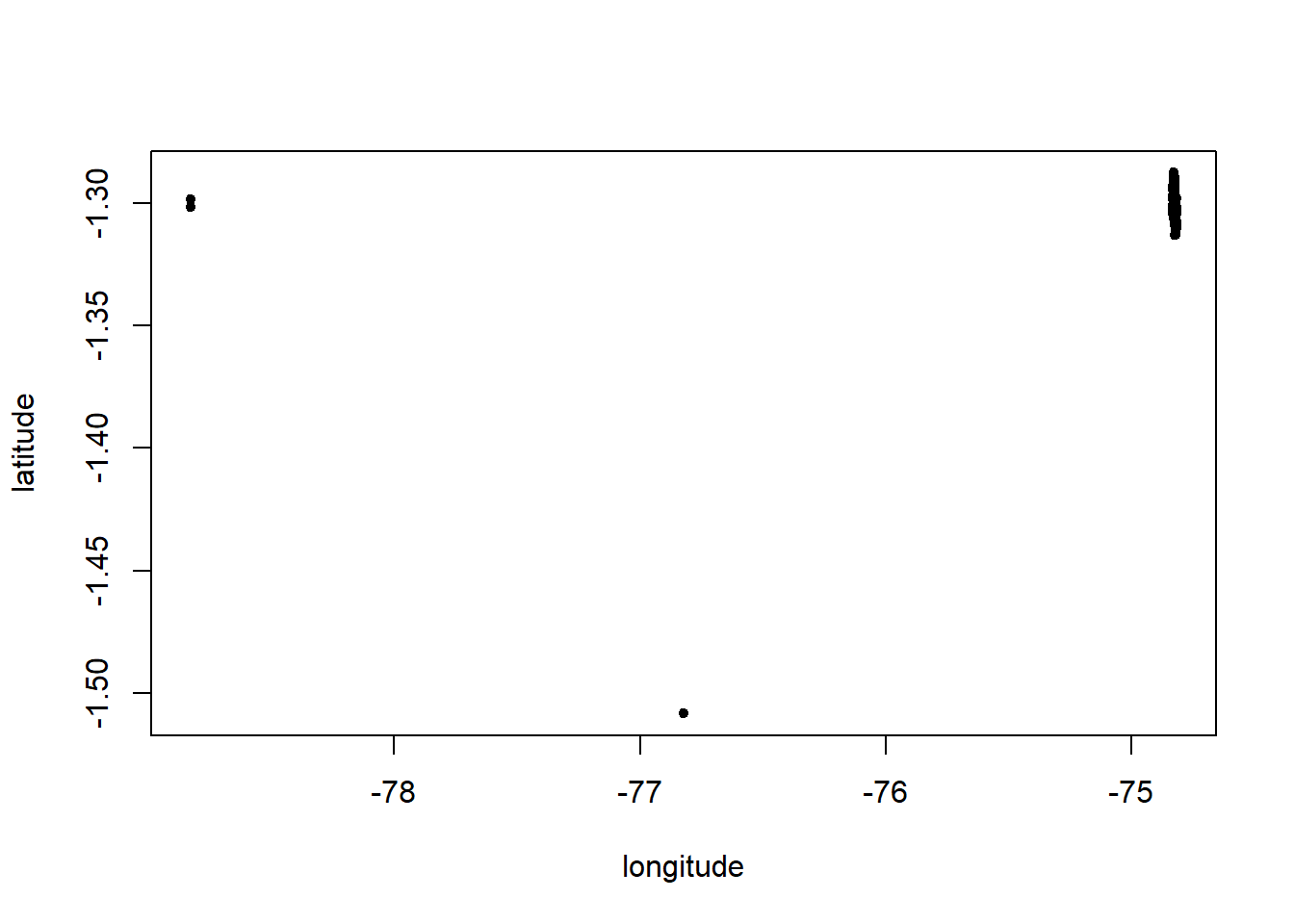
Ejercicio
Realiza una limpieza de este set de datos, elimina outliers y datos faltantes, y crea un objeto que contenga únicamente a “juancho”. Finalmente, verifica que el proceso haya sido exitoso.
# Verificación visual
library(plotly)
mamiferos_outliers <- mamiferos %>%
ggplot(aes(x= longitude, y=latitude, colour = name))+
geom_point(alpha = 0.5)
ggplotly(mamiferos_outliers)Con los gráficos interactivos de plotly puedes usar el cursor para observar la posición exacta de los outliers. Si bien esto es de utilidad para un set de datos pequeño como este, puedes automatizar tu código para deshacerte de todos aquellos puntos menores a la longitud -76.
#Limpiar el data frame
juancho <- mamiferos[-which(mamiferos$longitude < -76),] |>
na.omit() |>
filter(name == "juancho")Ahora que has filtrado el set de datos, ya puedes realizar la proyeccion, transformación y cálculo del área de vida y núcleo de juancho.
juancho.proj <- SpatialPointsDataFrame(coords = as.data.frame(cbind
(juancho$longitude, juancho$latitude)),
data = juancho, proj4string = CRS("+proj=longlat +ellps=WGS84 +datum=WGS84 +no_defs"))A diferencia de las zebras, sabemos que nuestro lugar de muestreo es pequeño, y en una región tropical, por ende necesitamos un método de proyección adecuado. Entre tantos métodos existentes, ¿cuál elegirías? En estos casos, lo aconsejable es utilizar Universal Transverse Mercator (UTM). No obstante, para hacer uso de este método de proyección, aún nos falta conocer un dato importante, la zona y el hemisferio.
Podemos copiar y pegar cualquiera de los puntos de nuestro set de datos en esta página para poder conocer la información faltante.
juancho.transf <- spTransform(juancho.proj,
CRS("+proj=utm +south +zone=18 +ellps=WGS84"))Si deseas conocer las coordenadas UTM de todos los puntos, puedes crear un nuevo objeto y ejecutar las siguientes líneas.
juancho.utm <- coordinates(juancho.transf)
head(juancho.utm)
## coords.x1 coords.x2
## [1,] 519037.6 9855961
## [2,] 518962.0 9855943
## [3,] 518962.0 9855956
## [4,] 518958.6 9855959
## [5,] 518960.9 9855956
## [6,] 518966.4 9855952
Ejercicio
Estima el área de vida (90%) y núcleo (50%) de juancho mediante el método MCP y realiza un gráfico mostrando ambos polígonos y puntos satelitales.
juancho.mcp.90 <- mcp(juancho.transf[, "name"], percent = 90,
unin = "m", unout = "ha")
juancho.mcp.50 <- mcp(juancho.transf[, "name"], percent = 50,
unin = "m", unout = "ha")Tal como lo hiciste para el set de datos de zebras, puedes transformar los objetos SpatialPolygonsDataFrame a un objeto sf para graficarlo fácilmente.
ggplot() +
geom_sf(data = st_as_sf(juancho.mcp.90),
color = "NA",
fill = "black",
alpha = 0.2) +
geom_sf(data = st_as_sf(juancho.mcp.50),
color = "NA",
fill = "purple",
alpha = 0.5) +
geom_sf(data = st_as_sf(juancho.transf), alpha = 0.5) +
coord_sf() +
labs(title = "Áreas de vida y núcleo de juancho estimadas mediante MCP") +
theme_bw()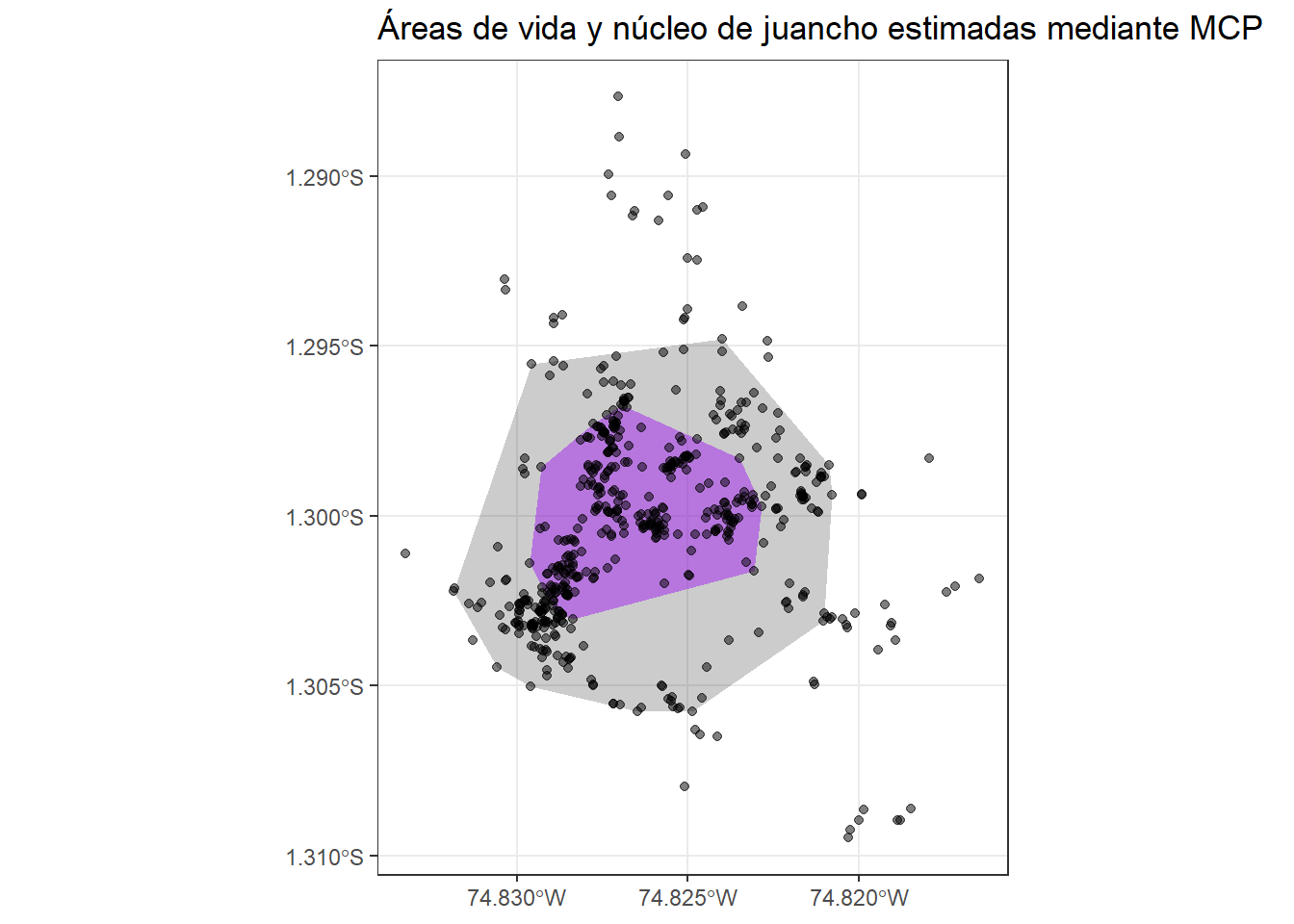
4.3 Kernel Density Estimate (KDE)
En KDE, una colina tri-dimensional o kernel es formada junto a cada punto, la forma y altura de esta colina depende del ancho de banda (bandwidth). En este curso calcularás el KDE mediante el “fixed kernel” o href, “least squares cross-validation” o lcsv, e intentarás ajustar el bandwidth manualmente. La teoría sobre estos métodos, sus pros y contras pueden ser encontrados en estos links: [1], [2].
4.3.1 Fixed kernel (href)
juancho.khref <- kernelUD(juancho.transf[, "name"], h = "href")
# Observa este raster
image(juancho.khref)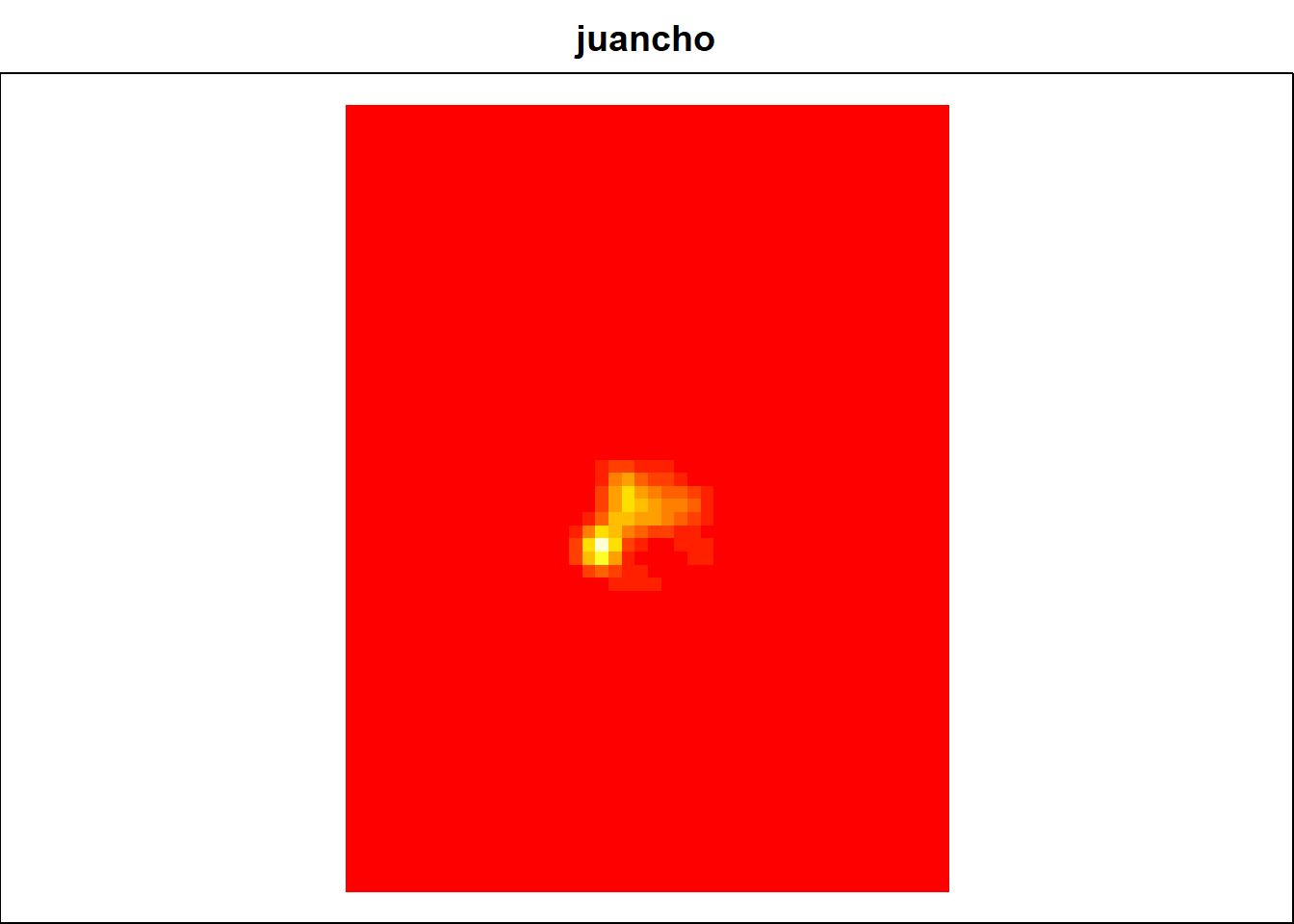
Si quieres exportarlo para su uso en otros softwares como ArcGis puedes seguir estos pasos.
juanchopix <- estUDm2spixdf(juancho.khref)
st_write(st_as_sf(juanchopix), "juancho.shp", delete_layer = TRUE)
# Mira otros formatos disponibles con st_drivers()También puedes plotearlo en R.
# Tambien lo puedes graficar en R
plot(juanchopix)
plot(juancho.transf, add = T, cex = 0.1)Utilizando estos objetos, ya puedes estimar el área de vida de juancho mediante el método KDE.
# Estimo el area usando el objeto juancho.khref segun una secuencia de porcentajes
kernel.area(juancho.khref, percent = seq (20, 95, 5),
unin="m", unout="ha")
## juancho
## 20 10.51807
## 25 15.02581
## 30 18.03098
## 35 22.53872
## 40 27.04646
## 45 31.55421
## 50 37.56453
## 55 43.57486
## 60 49.58518
## 65 58.60067
## 70 67.61616
## 75 79.63681
## 80 96.16520
## 85 117.20134
## 90 150.25813
## 95 204.35106Ahora puedes utilizar la función getverticeshr para obtener los polígonos que te permitirán graficar el área de vida y núcleo de juancho.
# Polígonos para el plot final
juancho.KDE90 <- getverticeshr(juancho.khref, percent = 90)
juancho.KDE50 <- getverticeshr(juancho.khref, percent = 50)
# Usa ggplot para graficar
ggplot() +
geom_sf(data = st_as_sf(juancho.KDE90),
color = "NA",
fill = "black",
alpha = 0.2) +
geom_sf(data = st_as_sf(juancho.KDE50),
color = "NA",
fill = "purple",
alpha = 0.5) +
geom_sf(data = st_as_sf(juancho.transf), alpha = 0.5) +
coord_sf() +
labs(title = "Áreas de vida y núcleo de juancho estimada mediante KDE") +
theme_bw()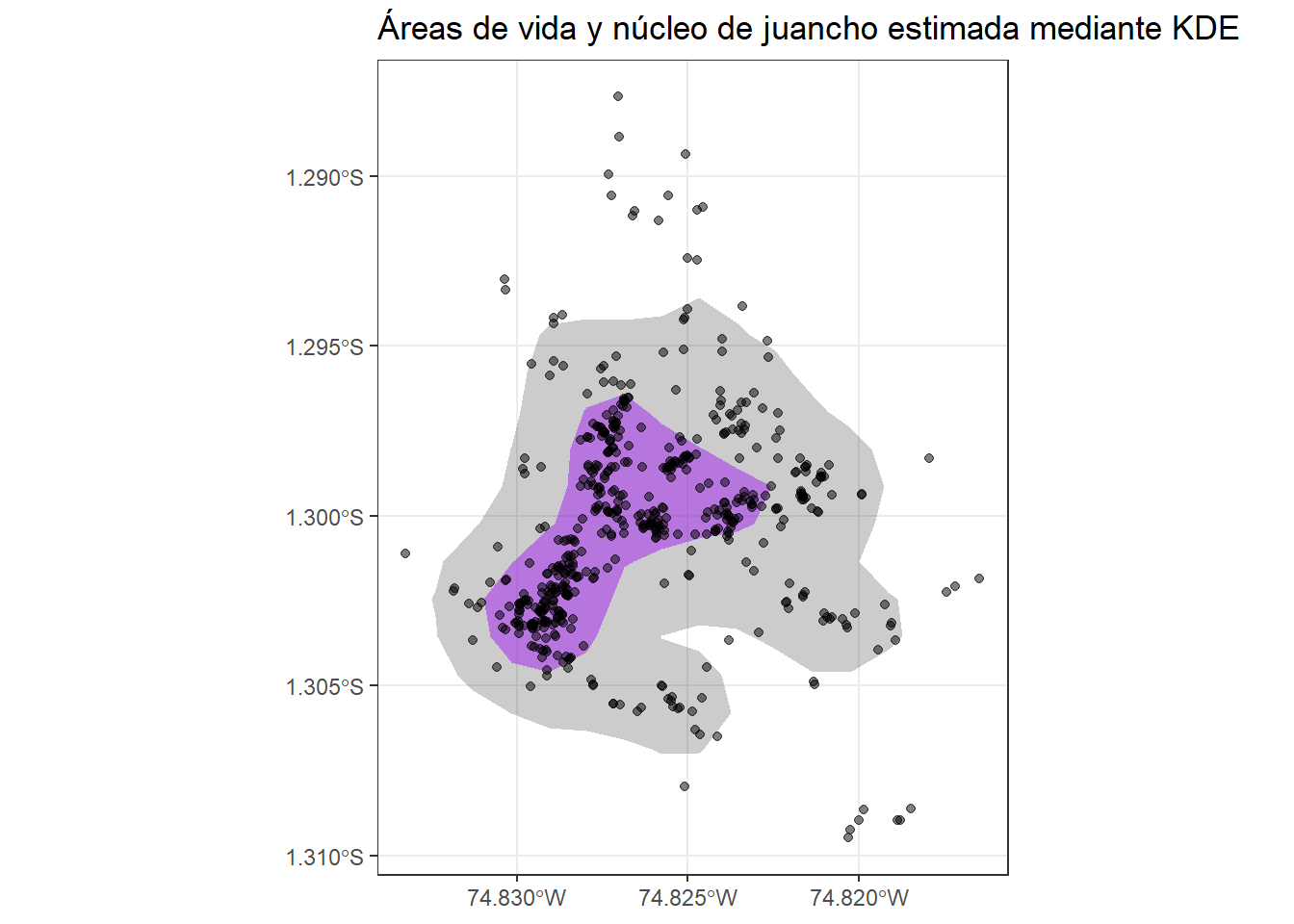
Ejericicio
La función getvolumeUD también te permite calcular el área de vida, pero ¿cuál crees que sea la diferencia entre ambos métodos?
4.4 Movebank
Con el advenimiento de nuevas tecnologías para el rastreo de animales, algunos problemas se hicieron evidentes debido al cumulo de información generada por los nuevos dispositivos. Esto conllevó al desarrollo del sistema Movebank, para poder mejorar el manejo del gran volumen y diversidad de información (Kays et al. (2022)).
Movebank es una plataforma web que permite almacenar datos de telemetría (GPS, Argos, VHF, etc) de manera privada y/o pública. A la fecha, cuentan con un total de 6 billones de locaciones generadas por más de 8 mil estudios que compreden a aproximadamente 1500 taxones. Además, almacena una gran diversidad de información asociada a cada proyecto (persona de contacto, grants, cita, licencia, etc), animal (Nombre, especie, peso, edad, etc) y a los sensores del collar (temperatura externa, altitud, frecuencia cardíaca, DOP, etc.
Estas variables han sido estandarizadas mediante lenguaje persistente, mediante una lista de vocabulario extensa que puede ser leído por máquinas y que está disponible en el Natural Environment Research Council’s Vocabulary Server (mira los detalles aquí).
El trabajo que realizarás a continuación utilizará una porción de los datos recolectados por Castellanos et al. (2022) de un zorro andino en Ecuador que puedes obtenerla aquí. Sin embargo, si quieres trabajar con las más de 6 mil posiciones satelitales, puedes acceder al repositorio de Movebank, o ingresar a www.movebank.org y buscar el proyecto “Home range and movement patterns of the Andean Fox in Cotopaxi National Park Ecuador”.
4.5 Autocorrelated Kernel Density Estimate (AKDE)
Lo descrito en esta sección es una parte muy pequeña de todo lo que puedes lograr con este paquete. Puedes encontrar mucho más en la página oficial de ctmm. Además, el grupo de google de ctmm es muy activo y encontrarás respuestas a posibles problemas que puedas tener con este paquete. La teoría sobre cada función ha sido publicada en varias revistas, y estas funciones se expandirán aún más en próximos años.
4.5.1 Error de posición
El primer paso en este flujo de trabajo es estimar el error de posición GPS. La explicación matemática de este parámetro se detalla en C. H. Fleming et al. (2020), acompañada por varias medidas de error de una gran variedad de collares. En caso de que no poseas información de calibración del collar o si no fuiste capaz de obtenerla, esta viñeta de R te explica un poco más sobre este proceso.
Aquuí usarás el error de calibración oportunista que se obtuvo tras la muerte del zorro andino Mashca.
calibracion <- read.csv("mashca_calibration.csv")
Ejercicio
Remueve los NA’s que se encuentran en las columnas de longitud y latitud del objeto calibracion.
Ahora plotea este objeto utilizando cualquiera de las columnas de posición.
plot(calibracion$utm.easting, calibracion$utm.northing)
Convierte este objeto a una nueva clase de objeto con la función as.telemetry. Asegúrate de saber cual es la zona horaria de tu lugar de estudio y del código EPSG, o puedes utilizar los argumentos projstring que utilizamos en Sección 3.2 para la transformaciónn a UTM.
library(ctmm)
calib.ctmm <- as.telemetry(calibracion, timezone = "America/Bogota", projection =
CRS("+init=epsg:32717"))
summary(calib.ctmm)
## $identity
## [1] "34811"
##
## $timezone
## [1] "America/Bogota"
##
## $projection
## [1] "+proj=utm +zone=17 +south +datum=WGS84 +units=m +no_defs"
##
## $`sampling interval (hours)`
## [1] 2.000833
##
## $`sampling period (months)`
## [1] 1.233174
##
## $`longitude range`
## [1] -78.44297 -78.43468
##
## $`latitude range`
## [1] -0.5536548 -0.5522826Ahora plotea este objeto, y compáralo con los gráficos anteriores. ¿Qué diferencias notas?
plot(calib.ctmm, error = 2)
Finalmente, debemos aplicar el error de locación al objeto calib.ctmm.
calib.model <- uere.fit(calib.ctmm)
summary(calib.model)
## , , horizontal
##
## low est high
## GPS-3D 8.511636e-04 0.3185801 0.8078993
## val. GPS-3D 3.448861e+01 36.1872461 37.8848005De esta manera, se puede estimar un error de posición de GPS de aproximadamente 36 metros. En este tutorial no removerás outliers, pero siempre es necesario aplicarlo a tu trabajo y encontrarás una explicación muy sencilla y directa sobre como hacerlo en la página oficial de ctmm.
Para mostrar los beneficios del uso del método AKDE, he separado el set de datos de mashca aproximadamente en dos mitades.
mashca_first <- read.csv("mashca_first_half.csv")
mashca_second <- read.csv("mashca_second_half.csv")Como es habitual, limpia estos objetos e importalos a ctmm tal como lo hiciste para la información de calibración.
mashca_first <- mashca_first[, c(3:5,8,9,15,18,19, 22)] %>%
na.omit() %>%
filter(gps.dop < 3, gps.fix.type.raw == "val. GPS-3D")
mashca_second <- mashca_second[, c(3:5,8,9,15,18,19, 22)] %>%
na.omit() %>%
filter(gps.dop < 3, gps.fix.type.raw == "val. GPS-3D")
# Importa a ctmm
mashca_first_ctmm <- as.telemetry(mashca_first, timezone = "America/Bogota",
projection = CRS("+init=epsg:32717"))
mashca_second_ctmm <- as.telemetry(mashca_second, timezone = "America/Bogota",
projection = CRS("+init=epsg:32717"))Puedes utilizar ctmm con listas, lo que mejorara tu flujo de trabajo cuando analices varios individuos.
# Une ambos objetos en una lista
mashca_merged <- list(mashca_first_ctmm, mashca_second_ctmm)
names(mashca_merged) <- c("first","second")
# Aplica el modelo de calibracion a la lista
uere(mashca_merged) <- calib.model
# Observa los datos
plot(mashca_merged[[2]], error=2)
4.5.2 Variogramas
El método implementado en ctmm requiere que los animales presenten un comportamiento de rango-residencia indicado por la función de semivarianza (SVF) de un proceso de movimiento estocástico, el cual puede ser visualizado mediante un variograma. Los detalles sobre este método se encuentran en Chris H. Fleming et al. (2014).
Debido a que los variogramas incorporan el efecto de tasa de muestreo para evaluar distintos comportamientos, es recomendable evaluar el intervalo en el cual los puntos de locación fueron tomados.
# Obtener grafico de intervalos
dt.plot(mashca_merged[[2]])
ablines = abline(h = c(1, 2, 4) %#% "hours", col = "red")
# Aplica este intervalo en un nuevo objeto
dt = c(c(2, 4) %#% "hours")
# Evalua el variograma
vg <- c()
for (i in 1:length(mashca_merged)){
vg[[i]] <- variogram(mashca_merged[[i]], dt)
}
# Puedes mirar este variograma como un gráfico estático o con zoom()
plot(vg[[2]], fraction = 0.9, level=c(0.5,0.95))
4.5.3 Model fitting
Tras incorporar el error de posición a los datos y seleccionar un variograma, debes realizar una aproximación empírica a lo que el modelo “pareceria ser”. Esto puede lograrse con la función guess.
# guess
guess <- c()
for (i in 1:length(mashca_merged)){
guess[[i]] <- ctmm.guess(mashca_merged[[i]],
variogram = vg[[i]],
interactive = FALSE)
guess[[i]]$error <- TRUE
}También puedes hacerlo manualmente si es que tienes el suficiente conocimiento sobre los parámetros que estás eligiendo.
ctmm.guess(mashca_merged[[1]],
variogram = vg[[1]])# Ajusta un modelo
fits_first <- ctmm.select(mashca_merged[[1]], CTMM = guess[[1]], trace = 3,
cores = 0)
fits_second <- ctmm.select(mashca_merged[[2]], CTMM = guess[[2]], trace = 3,
cores = 0)Puedes inspeccinar ambos objetos con summary y verás algo como esto:
## $name
## [1] "OU anisotropic error"
##
## $DOF
## mean area diffusion speed
## 221.6230 419.7824 788.3972 0.0000
##
## $CI
## low est high
## area (square kilometers) 7.973016 8.794272 9.655206
## τ[position] (hours) 4.624546 5.205921 5.860383
## diffusion (square kilometers/day) 4.031436 4.328335 4.635632
## error val. GPS-3D (meters) 34.474206 36.170462 37.865642En breve, ambos objetos muestran que no hay suficiente señal en la información para poder estimar velocidades no lineales ya que los grados de libertad de la velocidad son iguales a 0 y el modelo elegido fue OU anisotropic (lee Chris H. Fleming et al. (2014)). Sin embargo, hay suficiente información para estimar el área de vida de Mashca ya que los grados de libertad del área son 419.78.
4.5.4 AKDE
Para estimar la utilización de distribución de la primera mitad de datos de mashca:
mashca_first_akde <- akde(mashca_merged[[1]], fits_first,
trace = 2)
summary(mashca_first_akde, level.UD = 0.95)
Ejercicio
Calcula el AKDE para la segunda mitad de los datos de mashca. ¿Hay alguna diferencia?
Finalmente, puedes realizar un plot de estas áreas.
par(mfrow=c(2,2))
plot(mashca_merged[[1]], UD = mashca_first_akde,
col.grid=NA, level.UD= 0.5, error=2, main = "Primera mitad AKDE core mashca")
plot(mashca_merged[[2]], UD = mashca_second_akde,
col.grid=NA, level.UD= 0.5, error=2, main = "Segunda mitad AKDE core mashca")
plot(mashca_merged[[1]], UD = mashca_first_akde,
col.grid=NA, level.UD= 0.95, error=2, main = "Primera mitad AKDE core mashca")
plot(mashca_merged[[2]], UD = mashca_second_akde,
col.grid=NA, level.UD= 0.95, error=2, main = "Segunda mitad AKDE core mashca")
4.5.5 AKDE vs KDE
Realiza una comparación de ambos métodos y analiza sus semejanzas y diferencias. ¿Es uno de estos métodos mejor que el otro?
Tarea
Investiga como realicé los gráficos de las áreas de vida y núcleo estimadas con AKDE y KDE.
4.6 moveVis
Una excelente forma de atraer la atención a tus proyectos y de alcanzar a una audiencia no académica, es mostrando como el animal se desplaza por su área de vida sobre mapas satelitales. Es con este proposito que fue diseñado moveVis.
Ya que moveVis ha pasado por algunos cambios que no han sido cargados al repositorio de CRAN y este ha sido removido, te recomiendo descargar la versión 0.10.5 desde aquí. Este modo de instalación también puede requerir en algunos casos que instales ciertas dependencias primero por lo que te recomiendo que los instales de esta manera.
library(pacman)
p_load(move, slippymath, magick, gifski, av, pbapply, moveVis)Posteriormente, dirigete a la pestaña de Packages en R Studio y elige la opción Install en la esquina superior izquierda, y elige instalar desde un archivo .tar.gz. Ahora selecciona el directorio donde lo descargaste e instalalo.
Accede a Movebank y descarga el set de datos que utilizarás hoy para animar los movimientos de un jaguar muestreado en la Caatinga en Brasil. Para esto, ingresa al mapa y escribe “jaguar conservation in the caatinga biome”, elige el estudio y haz click en “Open in studies page”. Una vez aparezca la ventana que contiene todo acerca de este estudio, haz clic en “Download” y descarga este archivo en formato csv.
Debido a la gran cantidad de datos colectados en este estudio, selecciona solo a uno de los jaguares.
library(moveVis)
library(move)
library(tidyverse)
# Importa los datos
jaguars <- read_csv("Jaguars.csv")
# Selecciona a Courisco
courisco <- jaguars %>%
filter(`individual-local-identifier` == "Courisco")Ahora deberás llevar a cabo unos cuantos pasos para poder animar los movimientos de Courisco.
# Transformar en objeto move y selecciona una porcion de los datos
courisco_move <- df2move(courisco[1:500,],
proj = "+proj=longlat +south +zone=23 +ellps=WGS84",
x = "location-long", y = "location-lat", time = "study-local-timestamp",
track_id = "individual-local-identifier")Es importante saber cual es la frecuencia de muestreo antes de obtener los frames de la animacion.
# Visualizar frecuencia de muestreo
lagging <- timeLag(courisco_move,
unit="mins")
summary(lagging)
## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 58.00 60.00 60.00 68.06 60.00 540.00
# Histograma de frecuencias de muestreo
hist(lagging, xlab= "mins", xlim= c(0, 400), breaks= 40)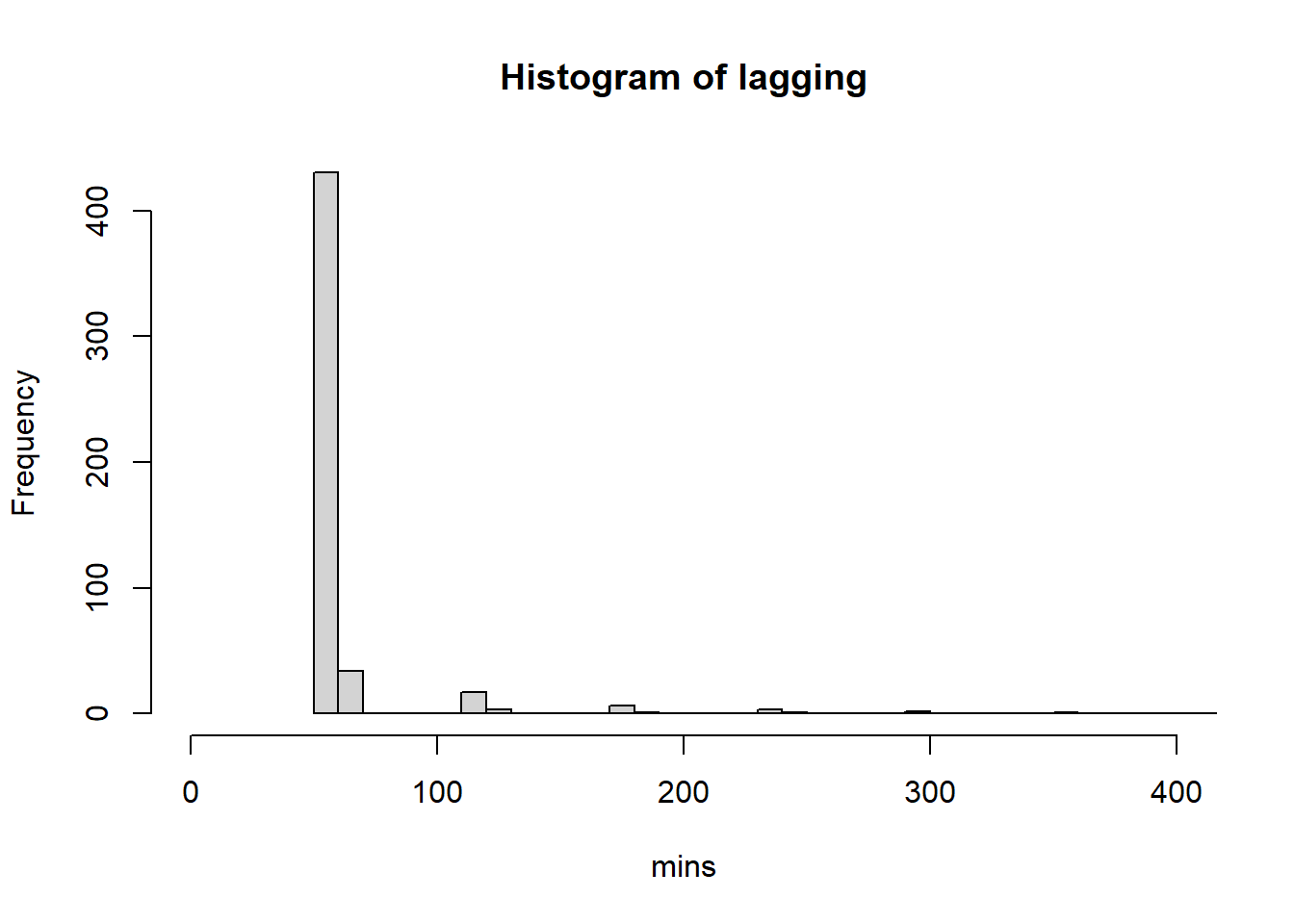
Utiliza el número estimado anteriormente para alinear y estandarizar la frecuencia de muestreo sobre el objeto.
courisco_move <- align_move(courisco_move, res = 60, unit = "mins")Hay una variedad de mapas que puedes utilizar como fondo para tu animación.
##ver mapas disponibles
get_maptypes()
## $osm
## [1] "streets" "streets_de" "streets_fr" "humanitarian" "topographic"
## [6] "roads" "hydda" "hydda_base" "hike" "grayscale"
## [11] "no_labels" "watercolor" "toner" "toner_bg" "toner_lite"
## [16] "terrain" "terrain_bg" "mtb"
##
## $carto
## [1] "light" "light_no_labels" "light_only_labels"
## [4] "dark" "dark_no_labels" "dark_only_labels"
## [7] "voyager" "voyager_no_labels" "voyager_only_labels"
## [10] "voyager_labels_under"
##
## $mapbox
## [1] "satellite" "streets" "streets_basic" "hybrid"
## [5] "light" "dark" "high_contrast" "outdoors"
## [9] "hike" "wheatpaste" "pencil" "comic"
## [13] "pirates" "emerald"También puedes indicar cuantos núcleos quieres utilizar para acelerar el proceso.
##utilizar nucleos
use_multicore()
use_multicore(n_cores = numero)Finalmente, utiliza el objeto alineado y estandarizado para obtener los frames.
# Crear el objeto que alamcene los frames de la animacion
frames <- frames_spatial(courisco_move,
map_service = "osm",
map_type = "topographic",
path_legend = F,
path_colours = "black",
path_alpha = 0.8,
tail_size = 2,
tail_length = 5)
frames[[535]]Puedes editar el formato de estas imágenes siguiendo el estilo de escritura de ggplot2.
frames_edit <- add_labels(frames, x = "Longitud" , y = "Latitud", verbose = TRUE) %>%
add_scalebar(height = 0.015) %>%
add_northarrow() %>%
add_timestamps(courisco_move, type = "label") %>%
add_gg(frames, gg = expr(labs(title = "Movimientos del jaguar Courisco en Brasil")))
frames_edit[[535]]Puedes mirar varios formatos para exportar la animación utilizando suggest_formats().
animate_frames(frames_edit, out_file = "courisco.gif",
height = 500, width = 500, res = 82, overwrite = TRUE)
4.7 Fuentes
Puedes utilizar el manual de adehabitatHR para resolver algunos ejercicios de este tutorial, y puedes explorar más funciones que también ofrece este paquete